📊 איך אפשר לדעת אם אלגוריתם יעיל באמת? ההבדל בין זמן פולינומי ל-זמן אקספוננציאלי הוא קריטי להבנת מגבלות כוח המחשוב. במאמר זה נסביר בצורה ברורה מה ההבדלים, נביא דוגמאות נפוצות, נציג טבלאות השוואה וגרף ויזואלי שימחיש את הפער העצום ביניהם.
מהו זמן פולינומי?
זמן פולינומי הוא מונח מתורת הסיבוכיות החישובית, המתאר זמן ריצה של אלגוריתם הגדל כפונקציה פולינומית של גודל הקלט. אם זמן הריצה ניתן לייצוג כ-O(n^k), כאשר n הוא גודל הקלט ו-k הוא קבוע, אז האלגוריתם נחשב לפועל בזמן פולינומי.
דוגמאות:
- מיון רשימה: אלגוריתמים כגון מיון מיזוג (merge sort) או מיון מהיר (quick sort) פועלים בזמן
O(n log n), הנחשב לזמן פולינומי. - מציאת מסלול קצר ביותר בגרף: אלגוריתם דייקסטרה (Dijkstra) פועל בזמן
O(n^2)אוO(n log n), תלוי במימוש.
מאפיינים:
- אלגוריתמים בזמן פולינומי נחשבים יעילים וישימים בפועל.
- בעיות שניתנות לפתרון בזמן פולינומי שייכות למחלקת הסיבוכיות P.
מהו זמן אקספוננציאלי?
זמן אקספוננציאלי הוא זמן ריצה של אלגוריתם הגדל באופן מעריכי (אקספוננציאלי) בהתאם לגודל הקלט. אם זמן הריצה הוא מהצורה O(k^n), כאשר k קבוע ו-n הוא גודל הקלט, אז מדובר בזמן אקספוננציאלי.
דוגמאות:
- בעיית הסוכן הנוסע (Travelling Salesperson Problem – TSP): פתרון על ידי בדיקת כל המסלולים האפשריים מצריך זמן
O(n!), שהוא גרוע אף יותר מזמן אקספוננציאלי. - חישוב כל תתי-הקבוצות האפשריות של קבוצה בגודל
nדורש זמןO(2^n).
מאפיינים:
- אלגוריתמים בזמן אקספוננציאלי נחשבים לא יעילים עבור קלטים גדולים, בשל קצב גידול זמן הריצה.
- בעיות שנפתרות רק בזמן אקספוננציאלי שייכות לרוב למחלקות NP-קשות או NP-שלמות.
השוואה בין זמן פולינומי לזמן אקספוננציאלי
| מאפיין | זמן פולינומי | זמן אקספוננציאלי |
|---|---|---|
| קצב גידול | איטי יחסית (n^2, n^3) | מהיר מאוד (2^n, n!) |
| דוגמאות לבעיות | מיון, מסלול קצר ביותר | בעיית הסוכן הנוסע, תתי-קבוצות |
| ישימות מעשית | ישים עבור קלטים גדולים | בלתי ישים אפילו עבור קלטים בינוניים |
| מחלקת סיבוכיות | P | NP-קשות, NP-שלמות |
למה זה חשוב?
זמן פולינומי:
- אלגוריתמים כאלה מסוגלים לעבד כמויות נתונים גדולות בפרק זמן סביר, ולכן הם שימושיים מאוד.
- בעיות הניתנות לפתרון בזמן פולינומי מהוות את הבסיס לרוב היישומים במדעי המחשב: עיבוד נתונים, רשתות, אלגוריתמים גרפיים, בינה מלאכותית ועוד.
זמן אקספוננציאלי:
- אלגוריתמים אלה הופכים לבלתי מעשיים אף עבור ערכי קלט קטנים יחסית.
לדוגמה, עבורn = 100, הביטוי2^100גדול יותר ממספר האטומים ביקום הנצפה. - לעיתים משתמשים בשיטות קירוב, היוריסטיקות או אלגוריתמים מקביליים כדי להתמודד עם בעיות כאלה בצורה מעשית.
דוגמה להשוואה מספרית
נניח שיש לנו בעיה שעלינו לפתור עבור n = 10 ו-n = 100:
זמן פולינומי: f(n) = n^2
n = 10:10^2 = 100פעולות.n = 100:100^2 = 10,000פעולות.
זמן אקספוננציאלי: f(n) = 2^n
n = 10:2^10 = 1,024פעולות.n = 100:2^100 ≈ 1.26 × 10^30פעולות.
🔎 המסקנה: אלגוריתם פולינומי נותר ישים גם בקלט גדול, בעוד אלגוריתם אקספוננציאלי הופך לבלתי ישים במהרה.
פונקציות נפוצות להמחשה
פונקציות פולינומיות
f(n) = n— עיבוד כל איבר פעם אחת (לינארית).f(n) = n^2— לולאות מקוננות, למשל מיון בועות.f(n) = n^3— עיבוד תלת-ממדי.f(n) = log n— חיפוש בינארי.f(n) = n log n— מיון מיזוג / מיון מהיר.
פונקציות אקספוננציאליות
f(n) = 2^n— סריקת כל תתי-הקבוצות האפשריות.f(n) = n!— סריקת כל התמורות (TSP).f(n) = 3^n— חישוב כל הקומבינציות האפשריות עם 3 מצבים.
דוגמת קוד להצגת גרף (Python, Matplotlib)
import matplotlib.pyplot as plt
import numpy as np
n = np.linspace(1, 20, 100)
# פונקציות פולינומיות
linear = n
quadratic = n**2
cubic = n**3
logarithmic = np.log(n)
nlogn = n * np.log(n)
# פונקציות אקספוננציאליות
exponential = 2**n
factorial = [np.math.factorial(int(i)) for i in n]
plt.figure(figsize=(10, 6))
plt.plot(n, linear, label='Linear: f(n) = n')
plt.plot(n, quadratic, label='Quadratic: f(n) = n^2')
plt.plot(n, cubic, label='Cubic: f(n) = n^3')
plt.plot(n, logarithmic, label='Logarithmic: f(n) = log n')
plt.plot(n, nlogn, label='Linearithmic: f(n) = n log n')
plt.plot(n, exponential, label='Exponential: f(n) = 2^n')
plt.plot(n, factorial, label='Factorial: f(n) = n!')
plt.yscale('log')
plt.xlabel('Input size (n)')
plt.ylabel('Time complexity')
plt.title('השוואה בין סיבוכיות פולינומית ואקספוננציאלית')
plt.legend()
plt.grid(True)
plt.show()מה ניתן ללמוד מהגרף?
- פונקציות פולינומיות גדלות בקצב מתון ונשארות נמוכות לאורך זמן.
- פונקציות אקספוננציאליות ממריאות במהירות ויוצאות משליטה עבור ערכים סבירים של
n. - שימוש בסקאלה לוגריתמית מאפשר הבחנה טובה יותר בין סוגי הפונקציות השונים.
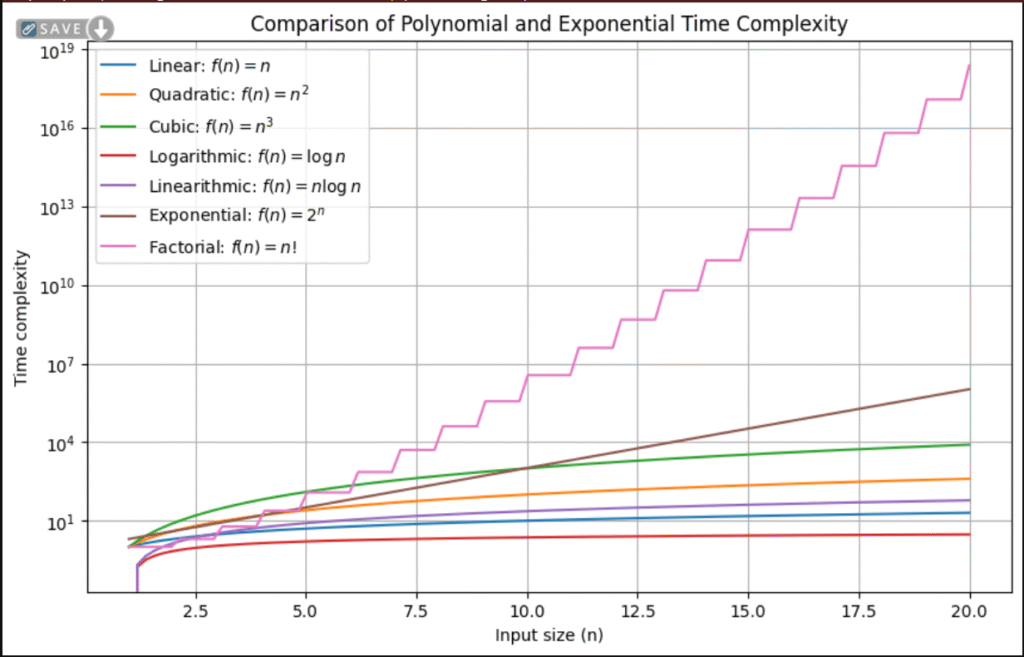
מה ניתן ללמוד מהגרף?
- פונקציות פולינומיות גדלות בקצב מתון ונשארות נמוכות לאורך זמן.
- פונקציות אקספוננציאליות ממריאות במהירות ויוצאות משליטה עבור ערכים סבירים של $n$.
- שימוש בסקאלה לוגריתמית מאפשר הבחנה טובה יותר בין סוגי הפונקציות השונים.